
记△ABC的内角A,B,C的对边分别为a.,b.,c,已知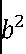 =ac,点D在边AC 上,BDsin∠ABC = asinC.
=ac,点D在边AC 上,BDsin∠ABC = asinC.
(1)证明:BD = b:
(2)若AD = 2DC .求cos∠ABC.


记△ABC的内角A,B,C的对边分别为a.,b.,c,已知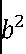 =ac,点D在边AC 上,BDsin∠ABC = asinC.
=ac,点D在边AC 上,BDsin∠ABC = asinC.
(1)证明:BD = b:
(2)若AD = 2DC .求cos∠ABC.

答案


扩展知识
一般的,在直角坐标系中,给定单位圆,对任意角α,使角α的顶点与原点重合,始边与x轴非负半轴重合,终边与单位圆交于点P(u,v),那么点P的纵坐标v叫做角α的正弦函数,记作v=sinα。通常,我们用x表示自变量,即x表示角的大小,用y表示函数值,这样我们就定义了任意角的三角函数y=sin x,它的定义域为全体实数,值域为[-1,1]。
相关公式
平方和关系
(sinα)^2 +(cosα)^2=1
积的关系
sinα = tanα × cosα(即sinα / cosα = tanα )
cosα = cotα × sinα (即cosα / sinα = cotα)
tanα = sinα × secα (即 tanα / sinα = secα)
倒数关系
tanα × cotα = 1
sinα × cscα = 1
cosα × secα = 1
商的关系
sinα / cosα = tanα = secα / cscα
和角公式
sin ( α ± β ) = sinα · cosβ ± cosα · sinβ
sin ( α + β + γ ) = sinα · cosβ · cosγ + cosα · sinβ · cosγ + cosα · cosβ · sinγ - sinα · sinβ · sinγ
cos ( α ± β ) = cosα cosβ ? sinβ sinα
tan ( α ± β ) = ( tanα ± tanβ ) / ( 1 ? tanα tanβ )
倍角半角公式
sin ( 2α ) = 2sinα · cosα [1]
sin ( 3α ) = 3sinα - 4sin & sup3 ; ( α ) = 4sinα · sin ( 60 + α ) sin ( 60 - α )
sin ( α / 2 ) = ± √( ( 1 - cosα ) / 2)
由泰勒级数得出
sinx = [ e ^ ( ix ) - e ^ ( - ix ) ] / ( 2i )
级数展开
sin x = x - x3 / 3! + x5 / 5! - ... ( - 1 ) k - 1 * x 2 k - 1 / ( 2k - 1 ) ! + ... ( - ∞ < x < ∞ )
导数
( sinx ) ' = cosx
( cosx ) ' = ﹣ sinx
查看答案
单次付费有效 3.99 元
用于查看答案,单次有效 19.99元
包月VIP 9.99 元
用于查看答案,包月VIP无限次 49.99元