
已知函数f(x)=x(1-lnx)
(1)讨论f(x)的单调性
(2)设a,b为两个不相等的正数,且blna-alnb=a-b证明: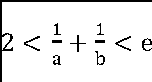


已知函数f(x)=x(1-lnx)
(1)讨论f(x)的单调性
(2)设a,b为两个不相等的正数,且blna-alnb=a-b证明: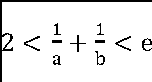

答案



扩展知识
函数的单调性(monotonicity)也叫函数的增减性,可以定性描述在一个指定区间内,函数值变化与自变量变化的关系。当函数f(x) 的自变量在其定义区间内增大(或减小)时,函数值也随着增大(或减小),则称该函数为在该区间上具有单调性(单调递增或单调递减) [1] 。在集合论中,在有序集合之间的函数,如果它们保持给定的次序,是具有单调性的。
如果说明一个函数在某个区间D上具有单调性,则我们将D称作函数的一个单调区间,则可判断出:
D?Q(Q是函数的定义域)。
区间D上,对于函数f(x),?(任取值)x1,x2∈D且x1>x2,都有f(x1) >f(x2)。或,? x1,x2∈D且x1>x2,都有f(x1) <f(x2)。
函数图像一定是上升或下降的。
该函数在E?D上与D上具有相同的单调性。
注意:函数单调性是针对某一个区间而言的,是一个局部性质。因此,说单调性时最好指明区间。
有些函数在整个定义域内是单调的;有些函数在定义域内的部分区间上是增函数,在部分区间上是减函数;有些函数是非单调函数,如常数函数。
函数的单调性是函数在一个单调区间上的“整体”性质,具有任意性,不能用特殊值代替。
在利用导数讨论函数的单调区间时,首先要确定函数的定义域,解决问题的过程中只能在定义域内,通过讨论导数的符号来判断函数的单调区间。
如果一个函数具有相同单调性的单调区间不止一个,那么这些单调区间不能用“∪”连接,而只能用“逗号”或“和”字隔开。
查看答案
单次付费有效 3.99 元
用于查看答案,单次有效 19.99元
包月VIP 9.99 元
用于查看答案,包月VIP无限次 49.99元