证明：如果两个三角形有两条边和其中一边上的中线对应相等，那么这两个三角形全等（提示：先分清已知和求证，然后画出图形，在结合图形用数学符号表示已知和求证．）
题目
可圈可点用户
2021-03-23 14:23
优质解答
答案
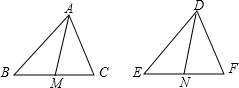
已知：△ABC和△DEF中，AB=DE，BC=EF，AM是△ABC的中线，DN是△DEF的中线，AM=DN，
求证：△ABC≌△DEF．
证明：∵BC=EF，AM是△ABC的中线，DN是△DEF的中线，
∴BM=EN，
在△ABM和△DEN中，
∵AB=DEBM=ENAM=DN ，
∴△ABM≌△DEN（SSS），
∴∠B=∠E，
在△ABC和△DEF中，
∵AB=DE∠B=∠EBC=EF，
∴△ABC≌△DEF（SAS）．
查看答案
可圈可点用户
2021-03-23 19:23
相关题库
下载试题
复制试题
最新题库
奇数中最小的合数是几
2021-03-23
已知甲=2×2×3，乙=2×3×5
2021-03-23
密度的国际单位
2021-03-23
12和18的最小公倍数
2021-03-23
美国本土西临什么洋
2021-03-23
美国的硅谷位于
2021-03-23
“硅谷”位于哪里
2021-03-23
根吸收水分和无机盐的最主要的部位是
2021-03-23
我国已满十八周岁的公民在符合宪法和法律规定的条件下应当积极行使什么
2021-03-23
艾滋病主要传播的途径v
2021-03-23
热门题库
下列食品中含碘量最少的是什么
2021-03-16
中国第一个共产党早期组织是在哪里成立
2021-03-17
我国旱涝灾害多的主要原因是
2021-03-21
什么的枫叶填合适词语
2021-03-17
中国共产党和各民主党派的关系是
2021-03-22
揭开人民解放战争全国性战略进攻序幕的是什么战役
2021-03-18
下列山脉属于我国第一阶梯和第二阶梯的界线的是
2021-03-17
大跃进运动的主要标志是
2021-03-17
新三民主义与旧三民主义相比较
2021-03-15
where are you going
2021-03-23
最新资讯
重庆大学强基计划招生简章2021 重庆大学强基计划
2021-04-02
高职高考可以报考哪些大学 3+证书可以考哪些大学
2021-04-02
教资出成绩2021 教资出成绩了吗
2021-04-02
出国留学专业如何选择 出国留学专业选择什么好
2021-04-02
重庆2021高职分类考试招生公布 重庆高职分类考试招生计划
2021-04-02
财政部招人需要什么专业 财政部怎么招人
2021-04-02
成考本科需要什么学历 第二学历和第一学历有什么区别
2021-04-01
初中生厌学怎么解决 初中生不想读书了怎么办
2021-04-01
2022年报考公务员的条件有哪些 适合考公务员的五大热门专业
2021-04-01
2021年执业医师考试时间安排 执业医师是什么级别
2021-04-01
热门资讯
教育改革2021最新消息 2021年教育改革内容
2021-03-18
第二轮双一流名单什么时候公布 2021双一流大学最新名单变更预测
2021-03-16
高考志愿填报技巧与指南2021 2021高考志愿填报指南
2021-03-19
四川大学华西临床医学院录取分数线2020
2021-03-15
2021北京沙尘暴原因 北京沙尘暴的原因是什么
2021-03-19
2021年江西普通高中学业水平考试报名系统及缴费
2021-03-21
青年大学习第十一季第二期答案截图 2021青年大学习最新答案
2021-03-22
中考分流政策2021 中考分流是什么意思
2021-03-16
上海学区房新政策2021 上海学区房改革最新消息
2021-03-17
高校经费排名2021全部榜单 教育部高校经费预算排名
2021-03-18
查看答案
限时优惠:
00时00分00秒
热门
单次付费有效 3.99 元
用于查看答案，单次有效 19.99元
微信扫码支付
包月VIP 9.99 元
用于查看答案，包月VIP无限次 49.99元
登录后扫码支付
微信扫码支付
去登陆