
已知数列{an}满足an+1=an+n,a1=1,则an=______.


已知数列{an}满足an+1=an+n,a1=1,则an=______.

∵an+1=an+n,a1=1,
∴a2-a1=1
a3-a2=2
…
an-an-1=n-1
以上n-1个式子相加可得,an-a1=1+2+…+n-1= 1+n-1/2 ×(n-1)= (n^2-n)/2
∴an= 1/2 n^2- 1/2 n+1
故答案为:an= 1/2 n^2- 1/2 n+1
数列求和的常用方法:
1.裂项相加法:数列中的项形如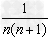 的形式,可以把
的形式,可以把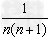 表示为
表示为 ,累加时抵消中间的许多项,从而求得数列的和;
,累加时抵消中间的许多项,从而求得数列的和;
2、错位相减法:源于等比数列前n项和公式的推导,对于形如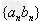 的数列,其中
的数列,其中 为等差数列,
为等差数列,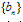 为等比数列,均可用此法;
为等比数列,均可用此法;
3、倒序相加法:此方法源于等差数列前n项和公式的推导,目的在于利用与首末两项等距离的两项相加有公因式可提取,以便化简后求和。
4、分组转化法:把数列的每一项分成两项,或把数列的项“集”在一块重新组合,或把整个数列分成两个部分,使其转化为等差或等比数列,这一求和方法称为分组转化法。
5、公式法求和:所给数列的通项是关于n的多项式,此时求和可采用公式求和,常用的公式有: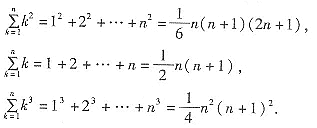
数列求和的方法多种多样,要视具体情形选用合适方法。
查看答案
单次付费有效 3.99 元
用于查看答案,单次有效 19.99元
包月VIP 9.99 元
用于查看答案,包月VIP无限次 49.99元